It means “random ramblings”. No, it’s not an actual word, but I’ve never understood why people keep words separate that are meant to be squished together. If you had a crocodile made out of chocolate, is it a chocolate crocodile? Obviously not – it’s a chocodile. Why does everybody always talk about stray dogs? They’re straynines. What if your sister likes to read the Communist Manifesto? Is she your Marxist sister? I think you get the idea. I suppose the ultimate opportunity for word squishification would occur if they decided to hold a chess tournament in Manchester, UK. It could be called the Manchesstournament. Anyway, this post isn’t truly randomblings, it’s a bunch of loosely connected mathematical ideas with no clear purpose – you could say pseudorandomblings.

Consider the simple linear function $f\left(x\right)=\frac{ax+b}{c}$. If we iterate $f$, we end up with a sequence of expressions like this:

$$x\tag{Iteration 0}$$

$$\frac{ax+b}{c}\tag{Iteration 1}$$

$$\frac{a\left(\frac{ax+b}{c}\right)+b}{c}=\frac{a^{2}x+ab}{c^{2}}+\frac{b}{c}\tag{Iteration 2}$$

$$\frac{a\left(\frac{a^{2}x+ab}{c^{2}}+\frac{b}{c}\right)+b}{c}=\frac{a^{3}x+a^{2}b}{c^{3}}+\frac{ab}{c^{2}}+\frac{b}{c}\tag{Iteration 3}$$

Each successive iteration, you replace $x$ with the result of the previous one. A clear pattern is emerging here, and it’s not so hard to see why. Every iteration, the degrees of $a$ in the numerators and the degrees of $c$ in the denominators all increase by one, with $b/c$ being added at the end. If you continue this pattern, the $n$th iteration is

$$\frac{a^{n}x}{c^{n}}+\frac{a^{n-1}b}{c^{n}}+\frac{a^{n-2}b}{c^{n-1}}+\cdots+\frac{b}{c}$$

$$=\left(\frac{a}{c}\right)^{n}x+\frac{b}{c}\sum_{k=0}^{n-1}\left(\frac{a}{c}\right)^{k}$$

That’s a messy, ugly looking expression. We can clean it up by considering for a moment just the summation. To make things work better, increase the upper index of the sum from $n-1$ to $n$ (this will be fixed later). The result is

$$\sum_{k=0}^{n}\left(\frac{a}{c}\right)^{k}$$

Expanding this out into terms:

$$\frac{a^{0}}{c^{0}}+\frac{a^{1}}{c^{1}}+\frac{a^{2}}{c^{2}}+\cdots+\frac{a^{n}}{c^{n}}$$

Now combine into a single fraction by multiplying each term with a power of $c$ divided by itself such that the denominator equals $c^n$:

$$\frac{a^{0}c^{n}+a^{1}c^{n-1}+a^{2}c^{n-2}+\cdots+a^{n}c^{0}}{c^{n}}$$

We can now apply the algebraic identity $$x^{n}-y^{n}=\left(x-y\right)\left(x^{n-1}+x^{n-2}y+\cdots+xy^{n-2}+y^{n-1}\right)$$ making the expression

$$\frac{a^{n+1}-c^{n+1}}{c^{n}\left(a-c\right)}$$

Plug this back into the original expression for the iteration of $f$ and readjust the index to get

$$\left(\frac{a}{c}\right)^{n}x+b\left(\frac{a^{n}-c^{n}}{c^{n}\left(a-c\right)}\right)$$

Much better, now there’s no intimidating summation symbol. Let’s call that expression $g(x,n)$. Based on the derivation of this formula that we just went through, you might think $g$ only makes sense for positive $n$. After all, how could $f$ be “composed” with itself a negative or non-integer number of times? Yet, the function takes on useful values even when $n$ is not a positive integer. First, let $n\in\mathbb{Z}^{+}$ and take $g(x,-n)$:

$$g(x,-n)=\left(\frac{a}{c}\right)^{-n}x+b\left(\frac{a^{-n}-c^{-n}}{c^{-n}\left(a-c\right)}\right)$$

$$=\left(\frac{c}{a}\right)^{n}x+b\left(\frac{\frac{1}{a^{n}}-\frac{1}{c^{n}}}{\frac{1}{c^{n}}\left(a-c\right)}\right)$$

$$=\left(\frac{c}{a}\right)^{n}x+b\left(\frac{\frac{c^{n}}{a^{n}}-1}{a-c}\right)$$

$$=\left(\frac{c}{a}\right)^{n}x+b\left(\frac{c^{n}-a^{n}}{a^{n}\left(a-c\right)}\right)$$

$$=\left(\frac{c}{a}\right)^{n}x-b\left(\frac{c^{n}-a^{n}}{a^{n}\left(c-a\right)}\right)$$

It looks like $a$ and $c$ swapped places and the plus sign turned into a minus. Well, think about $f(x)$. If $f(x)=\frac{ax+b}{c}$, then $f^{-1}(x)=\frac{cx-b}{a}$. Notice how the same thing happened: $a$ is in the place of $c$ and $b$ got negated. This means that letting $n$ be a negative integer corresponds to composing the inverse of $f$ with itself $n$ times.

We can even extend $g$ to non-integers. To do this, simply plug a number in that is not an integer. There is nothing that will cause the function to be undefined. This is a way to extend the intuitive meaning of $g$ (iterated composition) beyond just the integers. Such extension is commonplace in mathematics; for example, the gamma function extends the factorial and the Binet function extends the Fibonacci sequence. Using this idea, we can represent $g(x,n)$ as a surface by letting $n=y$. Here’s what that looks like if $f(x)=\frac{5x+3}{2}$:

Let’s now consider a special case for $g$. Suppose $c=a-1$. In this situation, $a-c=a-(a-1)=1$ so the denominator of the last part of $g$ simplifies to $c^n$. That leaves

$$\left(\frac{a}{c}\right)^{n}x+b\left(\frac{a^{n}-c^{n}}{c^{n}}\right)$$

$$=\left(\frac{a}{c}\right)^{n}+b\left(\left(\frac{a}{c}\right)^{n}-1\right)$$

$$=\left(\frac{a}{c}\right)^{n}\left(x+b\right)-b$$

Evidently, the expression is simplified considerably under this constraint. So what? Consider the Collatz conjecture (if you’re unfamiliar, it’s only a short read – I won’t redundantly explain it here). When the sequence reaches an odd number, the next term is given by 3 times the number plus 1. Since $3x+1$ is even for all odd $x$, the result will be divided by two. We can combine these two operations on the odd number $x$ to get $\frac{3x+1}{2}$. Look familar? This is in the form of $f(x)$, and even better, $c=a-1$. We can use that special case formula to get $g(x,n)$ when $f(x)=\frac{3x+1}{2}$:

$$g(x,n)=\left(\frac{3}{2}\right)^{n}\left(x+1\right)-1$$

For every $x$, there is a unique value $n$ such that $g(x,n)$ is an even number. The same number is the highest power of two that divides $x+1$. This $n$ is very interesting because it provides a notion of “how odd” an integer $x$ is. All positive odd numbers can be written as $2k+1$ for some $k\in\mathbb{N}$. We can call a number “more odd” if its value of $k$ is an odd number, and even moreso if $k_2$ is is an odd number where $k=2k_{2}+1$, and so on. For example, consider 15. 15 can be written as follows:

$15 = 2(7)+1 = 2(2(3)+1)+1 = 2(2(2(1)+1)+1)+1 = 2(2(2(2(0)+1)+1)+1)+1$

Since 15 had to be expanded in this manner 4 times, its associated “oddity” value is 4. Here’s the plot of the oddity value of the first 1000 odd numbers:

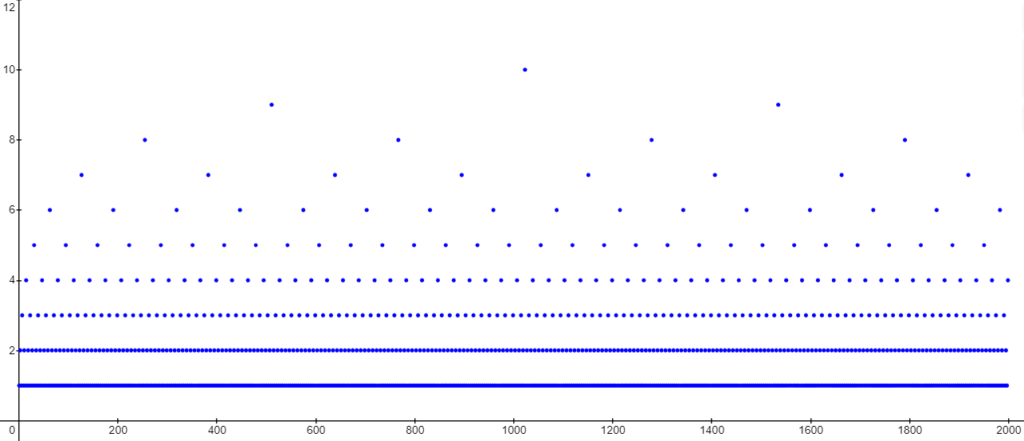
I was very surprised after seeing this, since it looks like a binary tree (to be fair, I had not yet realized oddity is equivalent to the highest power of 2 that divides $x+1$). After some consideration, though, it’s quite clear why it happens. The odd numbers can be constructed from $2k+1$ where $k=0,1,2,3,…$. Every other value of $k$ is even since every other natural number is even. The oddity value of $2k+1$ where $k$ is even will always be 1 because $g(2k+1,1)=3k+2$ which is even if and only if $k$ is even. That accounts for every other odd number. The reminaing odd numbers must have an odd value of $k$. The remaining $k$ values are ALL the odd numbers. Therefore, every other one of them will be one of the odd numbers with oddity 1. So, every four odd numbers has an oddity of 2. By the same reasoning, every 8 odd numbers will have oddity 3, and so on.

It is interesting to see how the transformation $(3x+1)/2$ impacts the oddity of $x$ before it reaches an even number. As all even numbers will converge to 1 or eventually reach an odd number under the Collatz function, and because all powers of 2 decrease directly to 1, the Collatz conjecture is equivalent to the statement that all odd numbers eventually reach a power of 2. Using the idea of oddity, and how it is affected by the functions of the conjecture, I believe it is possible to construct a probabilistic argument for the Collatz conjecture. That might not result in an airtight proof, but it could provide some more understanding. I have worked on it quite a bit lately and I expect to come across something worth sharing. In fact, I do already have some interesting finds. However, in the interest of keeping this post short (they have a tendency to get much too lengthy), I won’t include my progress so far here. It will probably be the next post. Thanks for reading!