Creation of MathGraph3D (Part 3 – Coloring and Lighting)

Posted on February 7, 2021February 7, 2021 by Sam

This series focuses on the creation of the original version of my 3D plotting software MathGraph3D. The first part was about the overall structure of the software. The second part was concerned with all algorithms for smoothing and optimizing surfaces. This third part discusses coloring, lighting, and styling the objects that MathGraph3D plots. I'll try to keep this part shorter than the other ones... posts in this series have a tendency to spiral out of control. In MathGraph3D, every plotta...

Creation of MathGraph3D (Part 2 – Surface Algorithms)

Posted on February 5, 2021February 5, 2021 by Sam

Finally, after a few months of promising this post, here it is. This series focuses on the creation of the original version of my 3D plotting software MathGraph3D. The first part was about the overall structure of the software. This second part is concerned with all algorithms for smoothing and optimizing surfaces. The basic idea of writing a program to plot 3D surfaces isn't too difficult once you get all the 3D space handling techniques covered. A naive script would map a mesh of input poi...

The infamous Goat Problem; my fruitless efforts…

Posted on January 9, 2021January 9, 2021 by Sam

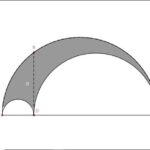
The Goat Problem is a centuries-old geometry problem with no closed form solution. If you tie a goat to the boundary of a circular fence that bounds 1 acre of area, how long does the rope need to be to allow the goat to roam exactly half of this area? Back in December 2020, Quanta Magazine posted a story announcing that Ingo Ullisch, a German mathematician, had reached the first exact solution. The trouble with this solution, however, is that it can only be evaluated iteratively. This is due to...

Collection of Desmos Graphs – Part 2

Posted on December 30, 2020January 2, 2021 by Sam

Just like last time, I'm going to share a few of my favorite recent graphs on Desmos. This is probably going to become a yearly thing - despite that the previous part was my first post ever, it remains the most popular. That's probably due to the fact that r/visualizedmath on Reddit won't let me post anymore to share my work. Anyway, on with the graphs... November 2019 MCC Puzzler Try it yourself: https://www.desmos.com/calculator/qsy5qk4sjv Last year, I took a couple math classes...

Project Euler – Number Spirals

Posted on December 4, 2020December 4, 2020 by Sam

Another Project Euler problem has sparked my attention. This one isn't particularly difficult (much less than the last one I posted about - despite being in the same category of difficulty), but it's an interesting problem with a nice solution. Most people probably don't approach this in the way I did, but for once I think my solution is cleaner than the others that are posted on the forum. The problem statement can be found here: Problem 28 Statement. Like last time, I'm going to proceed un...

Project Euler – Lattice Paths

Posted on December 4, 2020December 4, 2020 by Sam

Recently, I've been doing a bunch of Project Euler problems. If you're unfamiliar with Project Euler, it's a collection of challenging puzzles that require math and programming to solve. The puzzles are grouped by difficulty level. However, I've found that the difficulty can vary wildly within the same group. One challenge that stood out as much harder than the rest is Problem 15. The problem statement can be found here: Problem 15 Statement. Now, I'm going to continue under the assumption ...

Contour plots and their surface counterparts

Posted on November 7, 2020November 7, 2020 by Sam

This is mostly a gallery post, showing the contour plots and 3D surfaces of several functions. All of these images were made with MathGraph3D. f(x,y) = (sin(x) ^ 2) * (sin(y) ^ 2) * exp((x + y) / 2) / 3 + sin(x + y) / 4 on the region [-4,4] x [-4,4]. f(x,y) = sin(x + cos(2y)) - cos(y + sin(2x)) on the region [-2,2] x [-2,2]. f(x,y) = 1 + (x^3 + y^3) / 32 - 0.25x^2 on the region [-4,4] x [-4,4]. f(x,y) = sin(x + cos(y))sin(y + c...

Creation of MathGraph3D (Part 1 – Foundation)

Posted on September 21, 2020September 21, 2020 by Sam

This series focuses on the creation of the original version of my 3D plotting software MathGraph3D. This first part is concerned with the overall structural components of the software. Before getting into any actual algorithms or math, it’s necessary to set up an outline for how the code will be structured. I decided to create a manager class called “Plot” that would handle everything to do with 3D space and all objects in the calculator. There are five main operations that the Plot must be ...

Building a 3D Boat in Desmos

Posted on May 16, 2020December 14, 2020 by Sam

The graphing calculator Desmos recently held a competition called the Global Math Art Contest. People aged 13-18 submitted artwork they created with the graphing calculator using combinations of math curves. The judging is based on creativity, originality, visual appeal, and the math used to create the art. As a person with little artistic talent, I had to rely on the use of math category to get my edge. So I decided to create a rotatable 3D boat that moves and tilts according to the waves in t...

Common misconceptions about the differentiation operator

Posted on March 21, 2020May 30, 2020 by Sam

(Note: math may not render properly in Microsoft Edge. Any other browser should work, though. I'm trying to figure out the source of this issue.) This is the differentiation operator in single variable calculus: $$\frac{d}{dx}$$ Since several procedures in calculus happen to involve manipulating the "numerator" and "denominator" of the differentiation operator, people have gained the incorrect idea that it IS in fact a ratio of two "infinitely small" quantities. This is absolutely not tru...

sambrunacini.com

Author: Sam