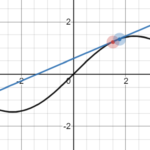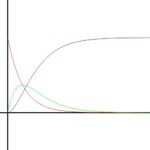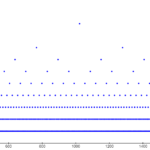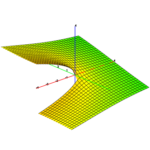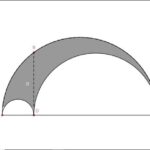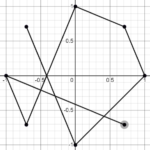
This isn't a novel idea, but I was looking for an iterative method for easing between two values. In this post, I describe and analyze the method of iterating a weighted arithmetic mean. I'm going to examine the effect of changing the weight factor and the rate at which the limiting value is approached as iterations increase. The end goal of this is to provide an alternative easing method to the standard parametric methods that use easing functions such as smoothstep or logistics. This allows t...
Read More